
eFatigue gives you everything you need to perform state-of-the-art fatigue analysis over the web. Click here to learn more about eFatigue.
き裂進展解析の技術背景
すべての疲労き裂は,非常に高い応力集中を生じます. 従来の解析法や材料特性は,き裂材の挙動を表現することはできませんので,その代わりに破壊力学が用いられます. 破壊力学は,き裂周囲の応力およびひずみ場を計算する一つの方法です. 等方性弾性材料にとって,き裂周囲の応力場を容易に計算することができます.
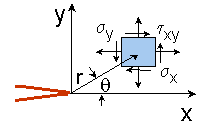
き裂先端からの位置を r と θ で表すと,応力場は下式で表されます.
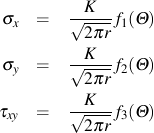
上式において,パラメータ K はき裂先端領域の応力場の増大を表すものであり,応力拡大係数と呼ばれます. 同じ応力拡大係数を持つ2つのき裂は,同じ挙動を示すことになります.
様々なき裂の応力拡大係数は一般に下式で表されます.
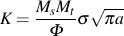
上式におけるそれぞれの項は,き裂長さ等のき裂形状と応力の負荷状態を表します.
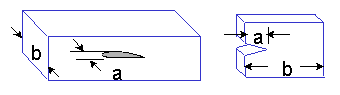
Ms は,表面き裂の修正係数です.右上図ような表面貫通き裂が一様な応力を受ける場合の Ms は Ms = 1.12 となります. 切欠きから生じた同じき裂の場合の Ms は Ms = 1.12 Kt で近似することができます. ここで,Kt は切欠きの応力集中係数です.表面き裂もまた,き裂のアスペクト比 a/2c に依存します. 複雑な応力分布とき裂形状は,複雑な修正係数 Ms を持ちます.
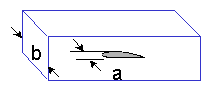
Mt は,き裂前方の自由表面における修正係数です.貫通き裂におけるこの修正係数は次式で与えられます.
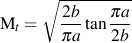
これは,き裂が成長する際に正味断面積の変化を表します. すなわち表面き裂において,き裂は a → b まで貫通して成長する過程において,そのアスペクト比は変化し続けることになります.
Φ はき裂のアスペクト比を表します.半円き裂は,貫通き裂が Φ = 1である間,Φ = π/2になります.
特殊な形状や特殊な応力状態における応力拡大係数は,一般に下式で表わされるように,それらのすべてを組合わせた効果から決定されます.
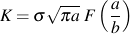
材料特性
き裂進展解析では,材料のき裂進展曲線(応力拡大係数範囲に対するき裂進展速度の関係)が必要になります. 材料のき裂進展曲線における線形部は,き裂の安定成長を表し,勾配 m と切片 C で表されます. 繰返しの応力拡大係数範囲 ΔK はき裂長さと作用する応力から計算されます.
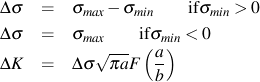
き裂進展速度は応力範囲とき裂サイズの両方に依存します.き裂は圧縮応力下では進展しないと仮定されます.
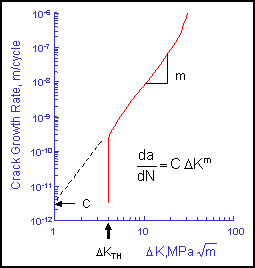
下限界応力拡大係数幅 ΔKTH はき裂が進展しない応力拡大係数の下限界値です. これは,従来の解析手法における疲労限度と類似しています. き裂は,初期き裂長さ ai と応力幅 Δs が下限界応力拡大係数幅よりも大きくなければ進展しません.
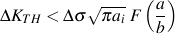
応力拡大係数
様々なき裂に対する応力拡大係数の一般的な形は下式で表されます.
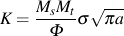
上式における各項は,き裂形状と応力の負荷形態を表します. 応力拡大係数Finder は,応力拡大係数を算出するために,負荷形態とき裂形状の組合せに応じた関数 F(a) を導き出します.
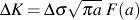
従来の応力集中係数 Kt と異なり,応力拡大係数はき裂サイズの関数です. したがって,応力拡大係数はき裂が大きくなるに従って増大します.一定応力レベルにおいても,き裂が長くなれば,き裂速度は増加してき裂成長は促進されます. 破壊力学において,き裂がない場合の応力は,全体的な断面の応力が採用されます.断面積減少の効果は,F(a)において表されます.
注意すべき点としては,正しいき裂長さを決定する場合に用いられなければならないことです. 表面き裂において,最も重要な寸法は,表面に沿った長さ 2c よりむしろき裂深さ a です. 表面き裂において最も損傷する箇所は,表面から見ることができない深さ方向のき裂先端です.ほとんどの表面き裂は,半楕円形状です.
幾つかのき裂は,き裂長さを a で表すよりむしろ 2a で表されます.
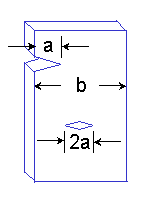
帯板表面の片側き裂は,自由表面とき裂先端を持ちますので,一方向にき裂は進展します. それに対して中央き裂は,2つのき裂先端を持ち自由表面はありません. この中央き裂の各方向のき裂成長は,b/2 の幅を持つ板が a の長さのき裂を持つように中央き裂の両端で進展します.
積分
初期き裂長さ ai からあるき裂長さ af までき裂を成長させるために要する繰返し負荷は,適切な応力拡大係数で材料のき裂成長速度を積分することによって導くことができます.
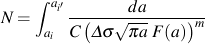
数値積分は,この積分を解くために用いられます.適切な初期き裂長さの選択には,機械構造物に関する若干の知識が必要です. 機械構造物は,しばしば1ミリオーダーのき裂を持っており,この事実は構造物において何も他に情報がない場合の取扱いに有効です. 疲労解析において,最終的なき裂長さはあまり重要ではありません.したがって,あらゆる合理的な評価法を用いても構いません.
 English
English